Messdatenbasierte Fahrdynamiksimulation
←
→
Transkription von Seiteninhalten
Wenn Ihr Browser die Seite nicht korrekt rendert, bitte, lesen Sie den Inhalt der Seite unten
Entwicklung Fahrdynamik Messdatenbasierte Fahrdynamiksimulation In der Fahrdynamiksimulation spielen die Eigenschaften der Achsen und Reifen die entscheidende Rolle. Dabei werden die Achsen meistens als Mehrkörpersysteme dargestellt. Bei dem messdatenbasierten Fahrdynamik- modell, das in der Pkw-Fahrwerksentwicklung bei Volkswagen verwendet wird, werden die Achsen, genauso wie die Reifen, vollständig durch Messdaten beschrieben. Die Achsdaten stammen aus Messungen auf dem Kinematik- und- Elastokinematik(KnC)-Messstand, die Reifendaten aus Flachbahn-Messungen. 274 AtZ 04i2009 Jahrgang 111
Die Autoren
1 Einleitung Dr.-Ing.
Chunyang Xie
Bekannte Merkmale der messdatenba- ist Entwicklungsinge-
sierten Modellierung sind Echtzeitfähig- nieur Pkw-Fahrwerk-
keit und Hardware-in-the-Loop (HiL)-Eig- Vorentwicklung der
nung. Weniger Beachtung findet bisher Volkswagen Ag in
die Nähe zum Versuch und zur Fahrwerks- wolfsburg.
abstimmung. Dazu kommt die ausge-
sprochene Benchmark-Tauglichkeit des
neuartigen Werkzeugs, denn die Daten- Dr. rer. nat.
gewinnung auf dem KnC-Messstand für Roland Altsinger
eigene und Wettbewerbsfahrzeuge bein- ist leiter Pkw-Fahr-
haltet den gleichen geringen Aufwand. werk-Vorentwicklung
In diesem Beitrag wird die Leistungsfä- der Volkswagen Ag in
higkeit der messdatenbasierten Fahrdy- wolfsburg.
namiksimulation mithilfe aufwendiger
Detailmessungen im Fahrbetrieb nach-
gewiesen. Dr.-Ing.
Die Kinematik und Elastokinematik Andreas Kunert
wird wie im Titelbild auf dem KnC-Mess- ist Senior Account
stand gemessen. Die Kinematik beschreibt Manager für Fahrzeug-
die Radbewegungen beim Federn und simulationsprogramme
beim Lenken. Die Elastokinematik be- bei der tesis Dynaware
schreibt Radstellungsänderungen durch gmbH in München.
Kräfte und Momente am Rad. Im Fahr-
betrieb überlagern sich Kinematik und
Elastokinematik.
Um reale Fahrmanöver bis in den
Grenzbereich hinein berechnen zu kön-
nen, ist eine Vielzahl spezieller Messpro-
zeduren auf dem KnC-Messstand auszu-
führen. Die komplette Bedatung eines dieser Tiefe erstmalig durchgeführte Ver-
Fahrwerks beinhaltet durch Überlage- messung soll die Überprüfung der Be-
rung einzelner Lastfälle zirka 180 Mes- rechnungsergebnisse bis hinein in die
sungen und dauert vier bis fünf Arbeits- Radstellungsänderungen und die Rad-
tage. Damit kann die Quer- und Längsdy- kräfte ermöglichen.
namik umfassend untersucht werden. Bei stationärer Kreisfahrt nehmen
Richtet sich die Fragestellung nur auf die Radlasten an den kurvenäußeren
Teilaspekte, zum Beispiel für Benchmark- Rädern mit der Querbeschleunigung li-
Zwecke auf die Querdynamik bei kons- near zu; kurveninnen nehmen sie dem-
tanter Fahrgeschwindigkeit, reduzieren entsprechend linear ab, Bild 1 oben
sich die Anzahl der Messungen und der links. Die Seitenkräfte an den Reifen
Zeitaufwand erheblich. steigen bis zirka 2 m/s² an allen Rädern
linear an, Bild 1 oben rechts. Darüber
nehmen sie kurvenaußen progressiv
2 Reifenkräfte und Radstellungen zu; kurveninnen ist der Seitenkraftzu-
im Fahrbetrieb wachs degressiv. Ab 6 m/s² nehmen die
Seitenkräfte innen sogar wieder ab. Bei
Um die Tauglichkeit der messdatenba- geringer Querbeschleunigung bis knapp
sierten Fahrdynamiksimulation zu un- 2 m/s² werden die Seitenkräfte von bei-
tersuchen, wurde ein Versuchsfahrzeug den Rädern einer Achse zu etwa glei-
mit Lenkmaschine, Messplattform, Cor- chen Teilen übertragen. Bei hoher Quer-
revits, Spurmessgerät und Kraftmessna- beschleunigung lasten die Achsseiten-
ben ausgerüstet und verschiedenen quer- kräfte zu mehr als 70 % auf den kurven-
dynamischen Tests unterzogen. Die in äußeren Rädern.
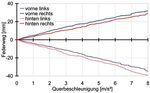
AtZ 04i2009 Jahrgang 111 275Entwicklung Fahrdynamik Bild 1: Oben links: Radlasten im 100-m-Kreis, Linksfahrt; oben rechts: Seitenkräfte im 100-m-Kreis, Linksfahrt; unten links: Federwege im 100-m-Kreis, Linksfahrt; unten rechts: Spurwinkel im 100-m-Kreis, Linksfahrt, die Spurwinkeländerungen der Vorderräder wurden um den Anteil des Lenkens bereinigt Die Federwegänderungen zeigen ein stärker aus als das kurveninnere Vorder- Hinterräder lenken annähernd parallel, Aufstützen und eine leichte Diagonalbe- rad: Das Fahrzeug vollführt eine Diago- kurvenaußen in Vorspur, kurveninnen wegung des Fahrzeugs, Bild 1 unten nalbewegung. in Nachspur. links. Die Einfederwege kurvenaußen Alle vier Räder zeigen fahrstabile un- Bei extremer Slalomfahrt wechseln sind geringer als die Ausfederwege kur- tersteuernde Spurwinkeländerungen, die übertragenen Hinterachsseitenkräfte veninnen. Das Fahrzeug stützt auf den Bild 1 unten rechts. Den größten Anteil in Bild 2 in Übereinstimmung mit Bild 1 Zusatzfedern auf. Das rechte, kurvenäu- leistet das kurvenäußere Vorderrad mit oben links und rechts zwischen maxima- ßere Vorderrad federt etwas stärker ein 54 min Nachspur bei 0,8 g Querbeschleu- len Werten bei hoher Radlast und mini- als das kurvenäußere Hinterrad. Das lin- nigung. Das kurveninnere Rad dreht malen Werten wenn die Vertikallast des ke, kurveninnere Hinterrad federt etwas dann um 15 min in Vorspur. Die beiden Rades gegen Null geht. Im Detail zeigt Bild 2: Radlasten und Seitenkräfte an den Hinterrädern bei extremer Slalomfahrt; Fahrgeschwindigkeit zirka 60 km/h 276 ATZ 04I2009 Jahrgang 111
Bild 3: Federwege und Spurwinkel an den Hinterrädern beim doppelten Fahrspurwechsel; Fahrgeschwindigkeit zirka 80 km/h
der dynamische Versuch zeitliche Ver- kinematik zeigt beispielhaft das wechsel- 4 Ergebnisse der Fahrdynamik
schiebungen zwischen Radlaständerung seitige Federn, Bild 4. Beide Achsen wer- simulation
und Seitenkraftaufbau. den in den Höhenständen leer, voll und
Der doppelte Fahrspurwechsel in Bild 3 1,5 Mal voll kraftgesteuert wechselseitig 4.1 Vergleich Messung mit Rechnung
ist ein weiteres extremes und hochdyna- bewegt. Dabei wird die jeweilige Achslast Der Vergleich von Messung und Rechnung
misches Fahrmanöver. Die Federwege konstant gehalten. An der Federbein-Vor- ist der Prüfstein jedes Rechenmodells. Die
sind dabei deutlich größer und unsym- derachse wird im Wesentlichen die glei- stationäre Kreisfahrt als anschaulichstes
metrischer als bei der stationären Kreis- che Spurkurve durchlaufen. Die Mehr- und einfachstes querdynamisches Fahrma-
fahrt, Bild 1 unten links. Die untersteu- lenker-Hinterachse zeigt ein kompli- növer eignet sich für den Vergleich beson-
ernden Spurwinkel an den Hinterrädern zierteres Bild. In jedem Höhenstand hat ders gut. Beim Vergleich wurde festgestellt,
sind fast doppelt so groß wie bei statio- diese Achse einen anderen Spurwert. dass die in Bild 1 dargestellten Radkräfte
närer Kreisfahrt mit 0,8 g, Bild 1 unten Von diesen unterschiedlichen Werten und -bewegungen gut zwischen Mes-
rechts. ausgehend entwickelt die Achse dann sungen und Berechnungen übereinstim-
die jeweilige wechselseitige Spurkurve. men. Diese gute Übereinstimmung erzielte
Als Beispiel für die Elastokinematik- man auch bei dynamischen Manövern,
3 Fahrzeugmodell und Achsbedatung Bedatung dient das Seitenkraftlenken an Bild 2 und Bild 3.
Vorder- und Hinterachse für verschie- Während die Radkräfte und -bewe-
Das Fahrzeugmodell basiert auf dem in dene Höhenstände, Bild 5. Die Spurände- gungen in gewissem Sinne Kontrollgrö-
Matlab/Simulink realisierten Programm rung durch Seitenkraft zeigt typisch für ßen für die Qualität der Modellbildung
„veDYNA“ der Firma Tesis Dynaware. Ein- die Federbeinachse eine weitgehende Hö- darstellen, stellen die Bewegungsgrößen
zelheiten dazu finden sich beispielswei- henstandsunabhängigkeit. Die Mehrlen- des Fahrzeugaufbaus die eigentlichen
se in [1]. Hier werden deshalb nur zwei kerhinterachse entwickelt umso mehr Zielgrößen der Berechnung dar. Die Qua-
kurze Beispiele zur Bedatung der Achsen Spuränderung durch Seitenkraft, je tief- lität der Berechnung der Aufbaubewe-
gezeigt. Die Vorgehensweise der Achs- er sie steht. gung wird anhand des anspruchsvollsten
Bild 4: Spurwinkel beim wechselseitigen Federn in drei Höhenständen; KnC-Messung
ATZ 04I2009 Jahrgang 111 277Entwicklung Fahrdynamik Bild 5: Seitenkraftlenken bei zwei Höhenständen; KnC-Messung Fahrmanövers, des doppelten Fahrspur- leichte Ungenauigkeiten in den Amplitu- der Radbewegung zu trennen: Das Rad wechsels, gezeigt, Bild 6. Dabei sind die den, der zeitliche Verlauf stimmt. Der hinten rechts lenkt beim doppelten Fahr- gemessenen Lenkradwinkel- und Fahrge- Schwimmwinkel und damit die Hinter- spurwechsel im Wesentlichen elastoki- schwindigkeitsverläufe die Eingangssig- achsbereifung und das Hinterachsspur- nematisch, Bild 7. nale der Rechnung. verhalten werden überzeugend getroffen. Ergänzend dazu zeigt Bild 8 die Kreis- Die Übereinstimmung zwischen Mes- Die Güte des Wankwinkels liegt auf dem fahrt des Beispielsfahrzeugs optional sung und Rechnung ist bei diesem kom- Niveau der Gierwinkelgeschwindigkeit. ohne elastokinematische Radstellungs- plizierten Fahrmanöver sehr gut. Die änderungen an der Vorderachse. Damit Rechnung liefert die gleichen hohen 4.2 Weitere Ergebnisbeispiele ist der Einfluss der dortigen Elastokine- Querbeschleunigungen wie die Messung. Das Simulationsmodell gestattet es, die matik auf das Lenkverhalten abzule- Die Gierwinkelgeschwindigkeit zeigt Kinematik- und Elastokinematikanteile sen. Bild 6: Berechnete Bewegungsgrößen des Fahrzeugaufbaus im Vergleich zur Messung; doppelter Fahrspurwechsel 278 ATZ 04I2009 Jahrgang 111
Entwicklung Fahrdynamik
Bild 7: Zerlegung des Spurwinkels rechts hinten in Kinematik- und Bild 8: Kreisfahrt im Serientrim und ohne Elastokinematik der Vorderachse
Elastokinematikanteil; doppelter Fahrspurwechsel
Bild 9: Stationäre Querdynamik von vier Pkw der unteren Mittelklasse; links: 100-m-Kreisfahrt; rechts: 0,4 g Gierverstärkung
Das Simulationsmodell erlaubt, Kenn- 5 Fazit Literaturhinweis
felder gezielt zu manipulieren. Durch [1] TESIS DYNAware: veDYNA Suspension Generator
Anpassung der gemessenen Spurweiten- Dieser Aufsatz dokumentiert das Poten- Manual, München, 2008
beziehungsweise Sturzwinkeländerung zial der messdatenbasierten Fahrdyna-
kann zum Beispiel die Momentanzen miksimulation. Das durch umfangreiche
trumshöhe der Achse variiert werden. kinematische und elastokinematische
Die anderen Achseigenschaften bleiben Messungen achsseitig exakt bedatete
dabei unverändert. Fahrzeugmodell liefert in Verbindung
mit einem hochwertigen Reifenmodell
4.3 Benchmark Querdynamikergebnisse nahe an der Re-
Die stationäre Kreisfahrt auf dem 100-m- alität. Hinsichtlich der Überlagerung von
Kreis und die stationäre Gierverstärkung Quer- und Längsdynamik muss dieser
bei 0,4 g Querbeschleunigung von vier Nachweis noch erfolgen.
Fahrzeugen der unteren Mittelklasse die- Dessen ungeachtet ist vorgesehen, die
nen als Beispiele für die Benchmarkfä- messdatenbasierte Fahrdynamiksimula-
higkeiten des auf KnC-Daten basierenden tion als Interpretationshilfe für KnC-Er-
Simulationsmodells, Bild 9. gebnisse bei der Fahrwerksabstimmung
zu verwenden und für vergleichende Ge-
genüberstellungen von KnC-Messungen
Download des Beitrags unter an eigenen und Wettbewerbsfahrwerken
www.ATZonline.de einzusetzen. Dieses wird genauere Bench-
Read the English e-magazine.
mark-Kennwerte und mittelfristig neue
Order your test issue now: Erkenntnisse bezüglich der Zielbereiche
SpringerAutomotive@abo-service.info
für Fahrwerksauslegungen liefern.
280 ATZ 04I2009 Jahrgang 111Sie können auch lesen